В инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности по тому или иному закону. Рассмотрим некоторые простейшие примеры распределенных сил, лежащих в одной плоскости.
Плоская система распределенных сил характеризуется ее интенсивностью q, т. е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры
1) Силы, равномерно распределенные вдоль отрезка прямой (рис. 69, а). Для такой системы сил интенсивность q имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей
По модулю,
Приложена сила Q в середине отрезка АВ.
2) Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 69, б). Примером такой нагрузки могут служить силы давления воды на плотину, имеющие наибольшее значение у дна и падающие до нуля у поверхности воды. Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения Равнодействующая Q таких сил определяется аналогично равнодействующей сил тяжести, действующих на однородную треугольную пластину ABC. Так как вес однородной пластины пропорционален ее площади, то, по модулю,
Приложена сила Q на расстоянии от стороны ВС треугольника ABC (см. § 35, п. 2).
3) Силы, распределенные вдоль отрезка прямой по произвольному закону (рис. 69, в). Равнодействующая Q таких сил, по аналогии с силой тяжести, по модулю равна площади фигуры ABDE, измеренной в соответствующем масштабе, и проходит через центр тяжести этой площади (вопрос об определении центров тяжести площадей будет рассмотрен в § 33).
4) Силы, равномерно распределенные по дуге окружности (рис. 70). Примером таких сил могут служить силы гидростатического давления на боковые стенки цилиндрического сосуда.
Пусть радиус дуги равен , где - ось симметрии, вдоль которой направим ось Действующая на дугу система сходящихся сил имеет равнодействующую Q, направленную в силу симметрии вдоль оси при этом численно
Для определения величины Q выделим на дуге элемент, положение которого определяется углом а длина Действующая на этот элемент сила численно равна а проекция этой силы на ось будет Тогда
Но из рис. 70 видно, что Следовательно, так как то
где - длина хорды, стягивающей дугу АВ; q - интенсивность.
Задача 27. На консольную балку А В, размеры которой указаны на чертеже (рис. 71), действует равномерно распределенная нагрузка интенсивностью Пренебрегая весом балки и считая, что силы давления на заделанный конец - определены по линейному закону, определить значения наибольших интенсивностей этих сил, если
Решение. Заменяем распределенные силы их равнодействующими Q, R и R, где согласно формулам (35) и (36)
и составляем условия равновесия (33) для действующих на балку параллельны сил
Подставляя сюда вместо Q, R я R их значения и решая полученные уравнения, найдем окончательно
Например, при получим а при
Задача 28. Цилиндрический баллон, высота которого равна Н, а внутренний диаметр d, наполнен газом под давлением Толщина цилиндрических стенок баллона а. Определить испытываемые этими стенками растягивающие напряжения в направлениях: 1) продольном и 2) поперечном (напряжение равно отношению растягивающей силы к площади поперечного сечения), считая малым.
Решение. 1) Рассечем цилиндр плоскостью, перпендикулярной его оси, на две части и рассмотрим равновесие одной из них (рис.
72, а). На нее в направлении оси цилиндра действуют сила давления на дно и распределенные по площади сечения силы (действие отброшенной половины), равнодействующую которых обозначим Q. При равновесии
Распределенные нагрузки
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
Размерность для линейной нагрузки - Н/м, для нагрузки распределенной по площади - Н/м 2 , для объемной (например при учете собственного веса элементов конструкции) - Н/м 3 .
Например, на рисунке 1.23, а приведена равномерно распределенная по длине , измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
Q = q ∙ AB [Н],
приложенной в середине отрезка AB .
На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
Q = q max ∙AB/2 ,
приложенной в точке C , причем AC = 2/3AB .
В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу
Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x) .
Рисунок 1.23
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).
Выделим элемент сектора с углом ∆φ и определим силу ∆Q , действующую на плоский элемент дуги:
∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ . (1.14)
Рисунок 1.24
Ox будет
∆Q x = q ∙ R ∙ ∆φ∙ cosφ . (1.15)
В силу симметрии элемента трубы (с дугой AB ) относительно оси Ox проекция результирующей силы на ось Oy :
Q y = 0 , т.е. Q = Q x , (1.16)
где АВ – хорда, стягивающая концы дуги.
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м, 2 ] . Если цилиндр рассечен по диаметру (рисунок 1.25), то равна F = q ∙ d ∙ h (d – внутренний диаметр) или
F = p ∙ 2R ∙ h .
Разрывающие баллон по диаметру усилия:
S 1 = S 2 = S;
2S = F;
S = p∙h∙R
. (1.18)
Поверхностные и объёмные силы представляют собой нагрузку, распределённую по некоторой поверхности или объёму. Такая нагрузка задаётся интенсивностью , которая представляет собой силу, приходящуюся на единицу некоторого объёма, или некоторой площади, или некоторой длины.
Особое место при решении ряда
практически интересных задач занимает
случай плоской распределённой нагрузки,
приложенной по нормали к некоторой
балке. Если вдоль балки направить ось
,
то интенсивность будет функцией
координаты
и измеряется в Н/м. Интенсивность
представляет собой силу, приходящуюся
на единицу длины.
Плоская фигура, ограниченная балкой и графиком интенсивности нагрузки, называется эпюрой распределённой нагрузки (Рис. 1.28). Если по характеру решаемой задачи можно не учитывать деформации, т.е. можно считать тело абсолютно твёрдым, то распределённую нагрузку можно (и нужно) заменить равнодействующей.
|
|
|
|
Разобьём балку на
отрезков длиной
,
на каждом из которых будем считать
интенсивность постоянной и равной
,
где
–координата отрезка
.
При этом кривая интенсивности заменяется
ломаной линией, а нагрузка, приходящаяся
на отрезок
,
заменяется сосредоточенной силой
,
приложенной в точке
(Рис. 1.29). Полученная система параллельных
сил имеет равнодействующую, равную
сумме сил, действующих на каждый из
отрезков, приложенную в центре
параллельных сил.
Понятно, что такое представление
тем точнее описывает реальную ситуацию,
чем меньше отрезок
,
т.е. чем больше число отрезков
.
Точный результат получаем, переходя к
пределу при длине отрезка
,
стремящейся к нулю. Предел, получаемый
в результате описанной процедуры,
представляет собой интеграл. Таким
образом, для модуля равнодействующей
получаем:
Для определения координаты точки
приложения равнодействующей используем
теорему Вариньона:
если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра (любой оси) равен сумме моментов всех сил системы относительно этого центра (этой оси)
Записывая эту теорему для системы сил
в проекциях на ось
и переходя к пределу при длине отрезков,
стремящейся к нулю, получаем:
Очевидно, модуль равнодействующей численно равен площади эпюры распределённой нагрузки, а точка её приложения совпадает с центром тяжести однородной пластины, имеющей форму эпюры распределённой нагрузки.
Отметим два часто встречающихся случая.
,
(Рис. 1.30). Модуль равнодействующей и
координата её точки приложения
определяются по формулам:
В инженерной практике такая нагрузка встречается довольно часто. Равномерно распределённой в большинстве случаев можно считать весовую и ветровую нагрузку.
|
|
|
|
(Рис. 1.31). В этом случае:
В
частности, давление воды на вертикальную
стенку прямо пропорционально глубине
.
Пример 1.5
Определить реакции опор
и
балки, находящейся под действием двух
сосредоточенных сил и равномерно
распределённой нагрузки. Дано:
|
|
Найдём равнодействующую распределённой нагрузки. Модуль равнодействующей равен
плечо силы
относительно точкиравно
Рассмотрим равновесие балки. Силовая
схема представлена на Рис. 1.33.
|
|
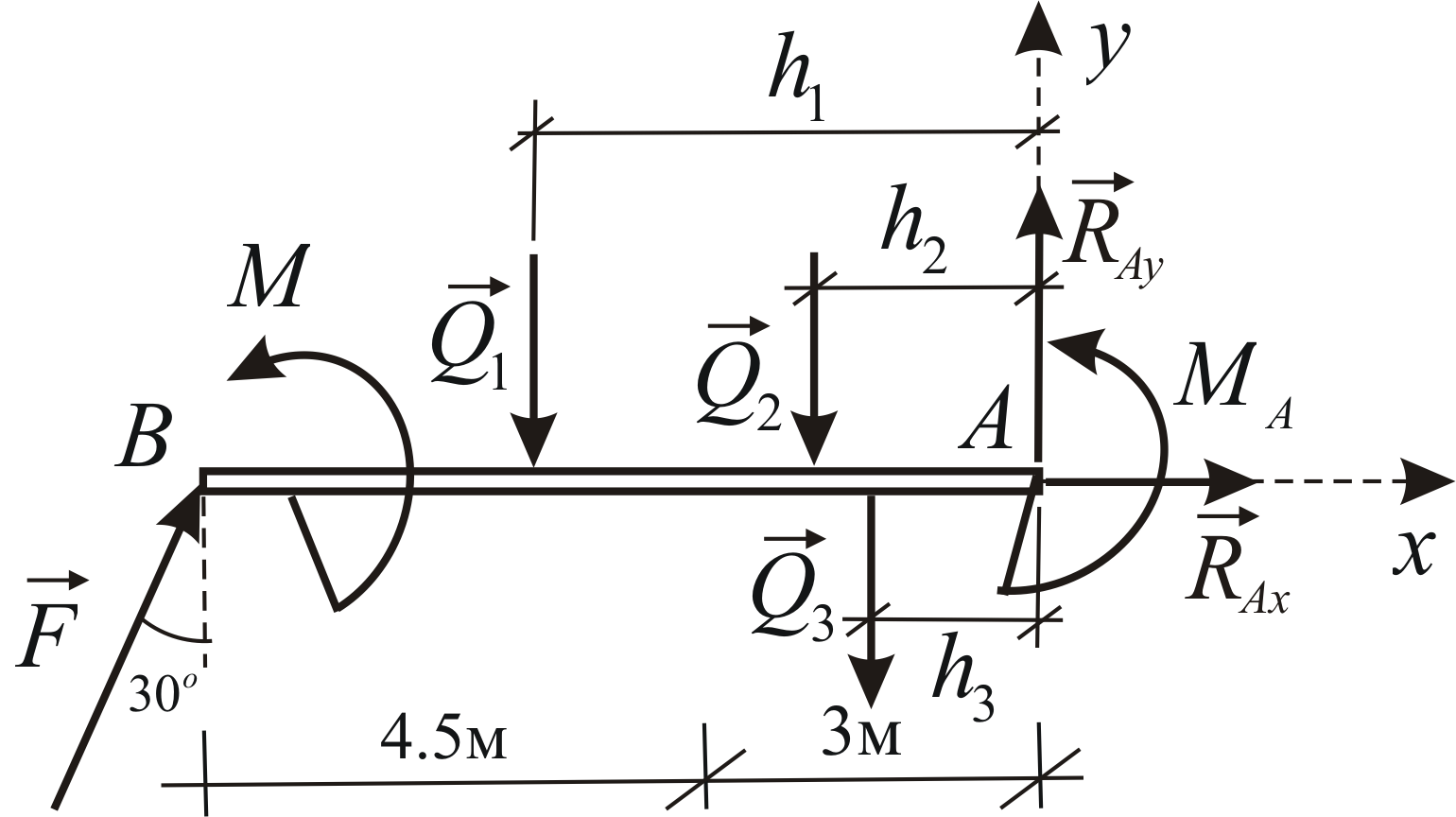
Пример 1.6
Определить реакцию заделки консольной балки, находящейся под действием сосредоточенной силы, пары сил и распределённой нагрузки (Рис. 1.34).
Заменим распределённую нагрузку тремя сосредоточенными силами. Для этого разобъём эпюру распределённой нагрузки на два треугольника и прямоугольник. Находим
Силовая схема представлена на Рис. 1.35.
|
|
|
|
Вычислим
плечи равнодействующих относительно
оси
Условия равновесия в рассматриваемом случае имеют вид:
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
1. Что называется интенсивностью распределённой нагрузки?
2. Как вычислить модуль равнодействующей распределённой нагрузки?
3. Как вычислить координату точки приложения равнодействующей распределённой
нагрузки?
4. Чему равен модуль и какова координата точки приложения равномерно распределённой нагрузки?
5. Чему равен модуль и какова координата точки приложения линейно распределённой нагрузки?
Из сборника задач И.В.Мещерского: 4.28; 4.29; 4.30; 4.33; 4.34.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-2; СР-3.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5
Распределенные нагрузки
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
Размерность для линейной нагрузки - Н/м, для нагрузки распределенной по площади - Н/м 2 , для объемной (например при учете собственного веса элементов конструкции) - Н/м 3 .
Например, на рисунке 1.23, а приведена равномерно распределенная по длине , измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
Q = q ∙ AB [Н],
приложенной в середине отрезка AB .
На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
Q = q max ∙AB/2 ,
приложенной в точке C , причем AC = 2/3AB .
В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу
Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x) .
Рисунок 1.23
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).
Выделим элемент сектора с углом ∆φ и определим силу ∆Q , действующую на плоский элемент дуги:
∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ . (1.14)
Рисунок 1.24
Ox будет
∆Q x = q ∙ R ∙ ∆φ∙ cosφ . (1.15)
В силу симметрии элемента трубы (с дугой AB ) относительно оси Ox проекция результирующей силы на ось Oy :
Q y = 0 , т.е. Q = Q x , (1.16)
где АВ – хорда, стягивающая концы дуги.
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м, 2 ] . Если цилиндр рассечен по диаметру (рисунок 1.25), то равна F = q ∙ d ∙ h (d – внутренний диаметр) или
F = p ∙ 2R ∙ h .
Разрывающие баллон по диаметру усилия:
S 1 = S 2 = S;
2S = F;
S = p∙h∙R
. (1.18)
Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно расстоянию между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки также попадают на начало и на конец пролета, но при этом вызывают только увеличение опорной реакции, на значение изгибающих моментов и на прогиб крайние сосредоточенные нагрузки никак не влияют, а потому при расчетах несущей способности конструкции не учитываются. Рассмотрим это на примере балок перекрытия опирающихся на перемычку. Кирпичная кладка, которая может быть между перемычкой и балками перекрытия, и создавать при этом равномерно распределенную нагрузку, для простоты восприятия не показана.
Рисунок 1 . Приведение сосредоточенных нагрузок к эквивалентной равномерно распределенной нагрузке.
Как видно из рисунка 1, определяющим является изгибающий момент, который используется при расчетах конструкций на прочность. Таким образом, чтобы равномерно распределенная нагрузка создавала такой же изгибающий момент, как и сосредоточенная нагрузка, ее нужно умножить на соответствующий коэффициент перехода (коэффициент эквивалентности). А определяется этот коэффициент из условий равенства моментов. Думаю, рисунок 1 это очень хорошо иллюстрирует. А еще, анализируя полученные зависимости, можно вывести общую формулу для определения коэффициента перехода. Так, если количество приложенных сосредоточенных нагрузок является нечетным, т.е. одна из сосредоточенных нагрузок обязательно попадает на середину пролета, то для определения коэффициента эквивалентности можно использовать формулу:
γ = n/(n - 1) (305.1.1)
где n - количество пролетов между сосредоточенными нагрузками.
q экв = γ(n-1)Q/l (305.1.2)
где (n-1) - количество сосредоточенных нагрузок.
Впрочем, иногда удобнее производить расчеты, исходя из количества сосредоточенных нагрузок. Если это количество выразить переменной m, то тогда
γ = (m +1)/m (305.1.3)
При этом эквивалентная равномерно распределенная нагрузка будет равна:
q экв = γmQ/l (305.1.4)
Когда количество сосредоточенных нагрузок является четным, т.е. ни одна из сосредоточенных нагрузок не попадает на середину пролета, то значение коэффициента можно принимать, как для следующего нечетного значения количества сосредоточенных нагрузок. В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:
γ = 2 - если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки.
γ = 1.33 - для балки, на которую действуют 2 или 3 сосредоточенные нагрузки;
γ = 1.2 - для балки, на которую действуют 4 или 5 сосредоточенных нагрузок;
γ = 1.142 - для балки, на которую действуют 6 или 7 сосредоточенных нагрузок;
γ = 1.11 - для балки, на которую действуют 8 или 9 сосредоточенных нагрузок.
2 вариант
Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно половине расстояния между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки не попадают на начало и на конец пролета.
Рисунок 2 . Значения коэффициентов перехода при 2 варианте приложения сосредоточенных нагрузок.
Как видно из рисунка 2, при таком варианте загружения значение коэффициента перехода будет значительно меньше. Так, например, при четном количестве сосредоточенных нагрузок, коэффициент перехода вообще можно принимать равным единице. При нечетном количестве сосредоточенных нагрузок для определения коэффициента эквивалентности можно использовать формулу:
γ = (m +7)/(m +6) (305.2.1)
где m - количество сосредоточенных нагрузок.
При этом эквивалентная равномерно распределенная нагрузка все также будет равна:
q экв = γmQ/l (305.1.4)
В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:
γ = 2 - если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки, а попадают ли балки перекрытия на начало или конец пролета или расположены сколь угодно далеко от начала и конца пролета, в данном случае значения не имеет. А значение это имеет при определении сосредоточенной нагрузки.
γ = 1 - если на рассматриваемую конструкцию, действует четное количество нагрузок.
γ = 1.11 - для балки, на которую действуют 3 сосредоточенные нагрузки;
γ = 1.091 - для балки, на которую действуют 5 сосредоточенных нагрузок;
γ = 1.076 - для балки, на которую действуют 7 сосредоточенных нагрузок;
γ = 1.067 - для балки, на которую действуют 9 сосредоточенных нагрузок.
Не смотря на некоторую заковыристость определения, коэффициенты эквивалентности очень просты и удобны. Так как при расчетах очень часто известна распределенная нагрузка, действующая на квадратный или погонный метр, то чтобы не переводить распределенную нагрузку сначала в сосредоточенную, а потом снова в эквивалентную распределенную, достаточно просто умножить значение распределенной нагрузки на соответствующий коэффициент. Например, на перекрытие будет действовать нормативная распределенная нагрузка 400 кг/м 2 , при этом собственный вес перекрытия составит еще 300 кг/м 2 . Тогда при длине балок перекрытия 6 м на перемычку могла бы действовать равномерно распределенная нагрузка q = 6(400 + 300)/2 = 2100 кг/м. А дальше, если будет только одна балка перекрытия посредине пролета, то γ = 2, а
q экв = γq = 2q (305.2.2)
Если ни одно из двух вышеприведенных условий не соблюдается, то использовать коэффициенты перехода в чистом виде нельзя, нужно добавить еще пару дополнительных коэффициентов, учитывающих расстояние до балок, не попадающих на начало и конец пролета перемычки, а также возможную несимметричность приложения сосредоточенных нагрузок. Вывести такие коэффициенты в принципе можно, однако в любом случае они будут понижающими во всех случаях, если рассматривать 1 вариант загружения и в 50% случаев, если рассматривать 2 вариант загружения, т.е. значения таких коэффициентов будут < 1. А потому для упрощения расчетов, а заодно и для большего запаса по прочности рассчитываемой конструкции вполне хватит коэффициентов, приведенных при первых двух вариантах загружения.
