Определить реакцию стержня шарнирно стержневой системы. Стержневые системы - реферат

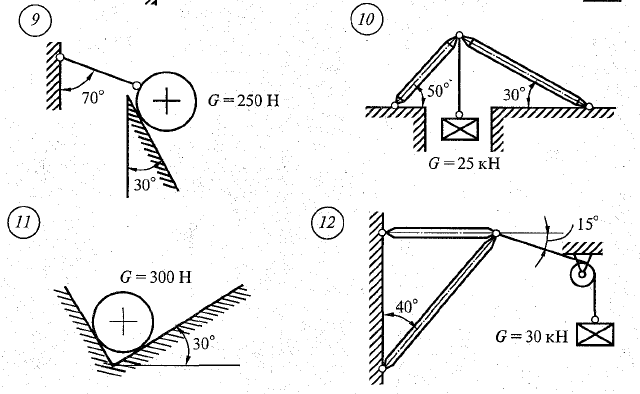
Задача №1. Определить реакции стержней, удерживающих грузы F 1 и F 2 . Массой стержней пренебречь. Схему для решения задачи выберете из таблицы 4, числовые данные - из таблицы 3, в соответствии с номером своего варианта

Задача №2. Горизонтальная балка, нагруженная силами F 1 и F 2 и парой с моментом М, удерживается в равновесии шарнирно-неподвижной опорой и шарнирно-подвижной опорой. Определить реакции в опорах балки. Весом балки пренебречь

Задача № 3.

Задача № 3. Схемы. Для ступенчатого стального бруса построить эпюры продольных сил и нормальных напряжений и проверить прочность каждого участка, приняв [σр]=150 Н/мм 2 , [σс]=120 Н/мм 2 . Определить перемещение свободного конца бруса. Модуль продольной упругости E=2×10 5 Н/мм 2

Задание для практической работы №4. Для тонкой однородной пластины, размеры которой даны в миллиметрах, определить положение центра тяжести

Задача № 5.

Задача № 5. Схемы. Привод состоит из электродвигателя мощностью Pдв с угловой скоростью ωдв и передачи, включающей редуктор и открытую передачу. Угловая скорость выходного вала ωвых. Требуется определить: а) общие КПД и передаточное отношение привода; б) передаточное число редуктора; в) мощности, угловые скорости и вращающие моменты на всех валах

Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).

Все связи можно разделить на несколько типов.

Связь - гладкая опора (без трения).Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).

Гибкая связь (нить, веревка, трос, цепь). Груз подвешен на двух нитях (рис. 1.8).

Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.

Жесткий стержень.

На схемах стержни изображают толстой сплош­ной линией (рис. 1.9).

Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня.

Стер­жень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.

Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допуска­ется в данный момент наложенными на него связями.

Убираем стержень 1, в этом случае стержень 2 падает вниз. Сле­довательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.

Шарнирная опора

Шарнир допускает поворот вокруг точки закрепления. Разли­чают два вида шарниров.

Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачивать­ся вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1.10).

Реакция подвижного шарни­ра направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной поверхности.

Неподвижный шарнир. Точка крепления переме­щаться не может. Стержень может свободно поворачи­ваться вокруг оси шарнира. Реакция такой опоры прохо­дит через ось шарнира, но неизвестна по направлению. Её принято изображать ввиде двух составляющих: горизонтальной и вертикальной (R x , Ry) (рис. 1.11).

Защемление или «заделка». Любые перемещения точки крепле­ния невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реак­тивный момент М R , препятствующий повороту (рис. 1.12).

Реактивную силу принято представ­лять в виде двух составляющих вдоль осей координат

R = R x + R y

Примеры решения задач

Последовательность решения задач:

1. Выбрать тело (точку), равновесие которого следует рассматри­вать.
2. Освободить тело (шарнир) от связей и изобразить действую­щие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира, так как принято предполагать, что стержни растянуты.
3. Выбрать оси координат и составить уравнения равновесия, ис­пользуя условия равновесия системы сходящихся сил на плоскости ∑Xi = 0; ∑Yi = 0. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей напра­вить перпендикулярно одной из неизвестных сил.
4. Определить реакции стержней из решения указанной системы уравнений.
5. Проверить правильность полученных результатов, решив уравне­ния равновесия относительно заново выбранных координат х и у.

Пример 1. Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1.13). Изобразить систему сил, действующих на шарнир А.

Решение

1. Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль нитей в сторону натяжения (рис. 1.13, а).

2. Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем воз­можные перемещения точки А.

Неподвижный блок с действующими на него силами не рассмат­риваем.

3. Убираем стержень 1, точка А поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене.

4. Убираем стержень 2, точка А поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.

5. Канат тянет вправо.

6. Освобождаемся от связей (рис. 1.13, б).

Пример 2. Шар подвешен на нити и опирается на стену (рис. 1.14а). Определить реакции нити и гладкой опоры (стенки).

Решение

1. Реакция нити - вдоль нити к точке В вверх (рис. 1.14, б).

2. Реакция гладкой опоры (стен­ки) - по нормали от поверхности опоры.

Пример 3. Представим, что на горизонтально расположенный брус АБ, собственной массой которого пренебрегаем, действует вертикальная нагрузка F, приложенная в точке С бруса (рис. 1.14-1, а). Левый конец бруса А прикреплен к опоре шарниром, а правый В опира­ется на гладкую наклонную плоскость.

Изобразим брус схематично отрезком АВ, как на рис. 1.14-1, б, и приложим к нему в точке С вертикальную силу F. В точке В со стороны наклонной плоскости к брусу приложена ее реакция R B , направленная перпендикулярно плоскости; линии действия сил F и R B пересекаются в точке О. Кроме этих сил на брус действует еще одна сила - реакция шарнирно-неподвижной опоры. А так как брус находится в равновесии, то линия действия третьей силы также пройдет через точку О, т. е. реакция R шарнир-но-неподвижной опоры направлена вдоль отрезка АО.

Примененный здесь метод рассуждения называется принципом освобождения тела от связей и замены связей их реакциями.

Пример 4. Определить усилие в стержне CD и силу давления груза А на опорную плоскость EF (рис. 1.14-2, а). Массой стержня CD, блока К, каната и трением каната о блок пренебречь.

Решение

Натяжение кана­та во всех его точках одина­ково и равно силе тяжести груза В, так как неподвиж­ный блок изменяет только направление силы, действую­щей на канат.

Рассмотрим равновесие си­стемы: стержень CD и блок К ML. Отбросим связи и заменим их действие соответствующими реакциями (рис. 1.14-2, 6). Для полученной системы сил можно соста­вить только одно уравнение равновесия:

На рис. 1.14-2, в показаны силы, действующие на груз А с прилегающим к нему отрезком каната ОН. R EF - реак­ция опорной плоскости.

Так как груз А находится в равновесии, то

R еf = Pa – Рв = 600 – 400 = 200 Н.

Сила давления груза А на опорную плоскость RA показана на рис, 1.14-2, г. Очевидно, R A = R EF = 200 H (сила действия равна силе противодействия).

Пример 5. Определить реакции стержней, удерживающих грузы F 1 = 70 кН и F 2 = 100 кН (рис. а). Массой стержней пренебречь.

Решение

1. Рассматриваем равновесие шарнира В (рис. а).

2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. б).

3. Выбираем систему координат, совместив ось у по направлению С реакцией R 2 (рис. б) и составляем уравнения равновесия для системы сил, действующих на шарнир В:

3. Определяем реакции стержней R 1 и R 2 , решая уравнения.

Подставляя найденное значение R 1 в уравнение (2), получаем

Знак минус перед значением R 2 указывает на то, что первоначально выбранное направление реакции неверное - следует направить реак­цию R 2 в противоположную сторону, т.е. к шарниру В (на рис. б истинное направление реакции R 2 показано штриховым вектором).

5. Проверяем правильность полученных результатов, выбрав новое расположение осей координат х и у (рис. а). Относительно этих осей составляем уравнения равновесия:

Значения реакций R 1 и R 2 , полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.

Контрольные вопросы и задания

1. Какая из приведенных систем сил (рис. 1.15) уравновешена?

4. Укажите возможное направление реакций в опорах (рис. 1.18).

Практическая работа 1

Тема: Определение реакций связей аналитическим и графическим способами.

Цель: Изучить виды связей, научиться определять их реакции.

Теоретическая часть:

Тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным .

Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным .

Все то, что ограничивает перемещения данного тела в пространстве, называется связью .

Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции связи или реакцией связи .

Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу.

Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей.

Все виды связей можно разделить на несколько типов.

1. Связь – гладкая опора (без трения).

Рисунок 1.1

Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рисунок 1.1).

2. Гибкая связь (нить, веревка, трос, цепь).

Реакция нити направлена вдоль нить от тела, при этом нить может быть только растянута (рисунок 1.2).

Рисунок 1.2

3. Жесткий стержень.

Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи (рисунок 1.3).

Рисунок 1.3

4. Шарнирная опора.

Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.

Подвижный шарнир . Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т.к. не допускается только перемещение поперек опорной поверхности

(рисунок 1.4).

Рисунок 1.4

Неподвижный шарнир. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Её принято изображать в виде двух составляющих: горизонтальной и вертикальной (рисунок 1.5).

Рисунок 1.5

5. Защемление или «заделка».

Любые перемещения точки крепления невозможны.

Реактивную силу принято представлять в виде двух составляющих вдоль осей координат (рисунок 1.6).

Рисунок 1.6

Пример.

Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рисунок 1.7).

Рисунок 1.7

1. Аналитический способ.

1. Определяем вероятные направления реакций. Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ – тянуть точку В к стене.

Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу – реакция направлена в верх.

2. Освобождаем точку В от связи.

3. Выберем направление осей координат, ось Ох совпадает с реакцией .

4. Запишем уравнения равновесия точки В:

5. Из второго уравнения получаем:

Из первого уравнения получаем:

2. Графический способ.

1. Выбираем масштабный коэффициент сил: µ = 1 Н/мм

Определяем отрезки, изображающие силы и :

,

.

2. Полученная система сил находится в равновесии, поэтому силовой

многоугольник должен быть замкнутым (рисунок 1.8).

Рисунок 1.8

3. Вычисляем реакции и , полученные в результате графического

Вычисляем погрешности:

.

Задание.

Аналитически и графически определить реакции связей, сравнить результаты.

Контрольные вопросы.

1. Что называется связью?

2. Перечислите основные виды опор.

3. Запишите аксиому связей.

4. Как направлена реакция гибкой нити?

1. Схема фигуры в масштабе

2. Решение

3. Ответы на контрольные вопросы

Практическая работа № 2

Тема: Определение реакций опор двух опорной балки.

Цель работы: Научится определять реакции опор балки установленной на двух опорах.

Теоретическая часть:

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

F 1x = F 1 cos α 1 > 0; F 2x = F 2 cos α 2 = - F 2 cos β 2 ;

cos α 2 = cos (180° - β 2)= - cos β 2

F 3x = F 3 cos90° = 0; F 4x = F 4 cos180° = - F 4 .

Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).

Определение равнодействующей системы сил аналитическим способом

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом.

Выберем систему координат, определим пропорции всех заданных векторов на эти оси (рис. 3.4, а).

Складываем проекции всех векторов на оси х и у (рис. 3.4, б).

Полнотекстовый поиск:

Главная > Реферат >Строительство

1. Кинематический анализ стержневых систем.

Свойство системы изменять форму при отсутствии приращений деформаций в ее элементах называется изменяемостью.

С кинематической точки зрения стержневые системы могут быть:

– геометрически неизменяемые , имеющие лишь необходимое количество связей для обеспечения неизменяемости – статически определимые стержневые системы ;

– геометрически неизменяемые , обладающие большим числом связей» чем это необходимо для обеспечения неизменяемости – статически неопределимые стержневые системы ;

– геометрически изменяемые.

Ограничимся кинематическим анализом плоских стержневых систем.

Положение плоской фигуры в ее плоскости определяется тремя независимыми параметрами (рис.2.1) двумя координатами некоторой точки В и углом наклона какой-либо прямой АВ . Отсюда следует, что плоская фигура в своей плоскости обладает тремя степенями свободы.

Стержневую систему представим в виде набора отдельных плоских фигур – жестких дисков, тем или иным способом соединенных друг с другом или основанием (рис. 2.2). Здесь под жестким диском понимаем комбинацию стерней, жестко соединенных между собой. Как было установлено выше, каждый жесткий диск обладает тремя степенями свободы. Всякое устройство, уничтожающее одну степень свободы, называется кинематической связью. Цилиндрический шарнир с неподвижной геометрической осью, вокруг которой диск может вращаться, эквивалентен двум связям. Вводится понятие кратного шарнира, при помощи которого соединяется более чем два диска. Он эквивалентен n -1 простым шарнирам, где n – число соединяемых дисков.

С учетом введенных понятий, легко построить формулу для определения числа степеней свободы любого сооружения:

W = 3 D – 2Ш – С 0 ,

D – число жестких дисков в стержневой системе;

Ш – число простых шарниров, при помощи которых соединены между собой простые диски;

С 0 – число опорных стержней, при помощи которых сооружение связано с землей.

Естественно, что необходимым условием обеспечения не­изменяемости системы является отсутствие у сооружения степеней свободы, т.е. W ≤ 0 . Однако выполнение указанного условия недостаточно для заключения о кинематической неизменяемости сооружения. Для проведения полного кинематического анализа, кроме выяснения числа степеней свободы сооружения, необходимо провести анализ геометрической структуры сооружения, т.е. способов образования стержневой системы.

Рассмотрим основные типы элементарных геометрически неизменяемых систем.

1. К двум дискам, связанным общим шарниром А присоединен при помощи двух шарниров В и С третий, причем, прямая, соединяющая оси шарниров В и С не пересекает точку А (рис. 2.3).

2. Два жестких диска соединены между собой при помощи трех стержней, оси которых не параллельны и не пересекаются в одной точке (рис. 2.4).

3. Два жестких диска соединены между собой при помощи одного шарнира и стержня, ось которого не пересекает шарнир (рис. 2.5).

В

последующем объектом исследований будет сооружение, для которого выполняется отсутствие степеней свободы (W ≤0 ) при подтверждении, в результате анализа его геометрической структуры, соблюдения правил образования геометрически неизменяемых систем.

Если геометрически неизменяемая система характеризуется равенством нулю степеней свободы (W =0 ), то она является статически определимой, т.е. для ее расчета достаточно одних уравнений равновесия. При наличии у геометрически неизменяемой системы дополнительных связей (W ), она является статически неопределимой и для ее расчета одних уравнений равновесия уже недостаточно.

2. Свойства статически определимых стержневых систем.

Основным свойством статически определимых стержневых систем, вытекающим из самого определения, является возможность нахождения опорных реакций, внутренних усилий исходя из уравнений равновесия.

Отсюда и из некоторых положений, установленных при рассмотрении стержневой системы как совокупности жестких дисков, можно сделать следующие выводы:

1. В статически определимых стержневых системах распределение внутренних усилий не зависит от поперечных размеров и материала стержней.

2. В статически определимых системах не возникают внутренние усилия вследствие изменения температуры, смещений (осадки) опор и неточности сборки.

3. Замена нагрузки на одном из дисков статически ей эквивалентной не приводит к изменению усилий в остальной части системы.

4. Изменение конфигурации какого-либо диска при сохранении связей его с остальной частью системы и с основанием не вызывает усилий в остальной части системы.

5. Нагрузка, приложенная к основной части стержневой сис­темы, не вызывает усилий в прикрепленных частях, но загружение прикрепленных частей приводит к возникновению внутренних усилий и в основной части сооружения.

6. Наиболее существенным недостатком статически определимых стержневых систем является отсутствие резерва геометрической неизменяемости, вследствие чего при разрушении одного из стержней возможно разрушение всей системы.

2.3. Основные принципы нахождения внутренних усилий в статически определимых стержневых системах.

1. Понятие о внутренних усилиях.

Основными искомыми в задачах строительной механики являются внутренние усилия, возникающие в сооружениях вследствие внешнего воздействия.

Рассмотрим следующий пример. Пусть стержень находится в равновесии под действием внешней нагрузки и возникающих опорных реакций (рис. 2.6). В результате действия внешних сил стержень деформируется, примет другую форму. При этом в каждой точке тела возникают силы, стремящиеся возвратить его в первоначальное положение. Действительно, если убрать внешнюю нагрузку, то стержень примет первоначальную форму. Надо только иметь в виду, что сказанное справедливо, если материал стержня работает в пределах упругости.

Для определения внутренних усилий, как нам известно из сопротивления материалов, используется метод сечений. Суть его заключается в том, что мысленно проводится сечение, рассекающее рассматриваемую стержневую систему на две части (так называемо замкнутое сечение). Этот прием позволяет "вскрыть" внутренние силы, рассмотрев равновесие любой из отсеченных частей стержневой системы под действием оставшейся на ней внешней нагрузки, опорных реакций и возникающими внутренними силами в самом сечении (рис. 2.7а).

Д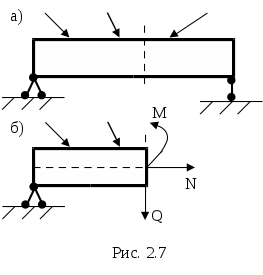ля удобства определения внутренних усилий, возникающих в каждой точке плоскости се­чения, приведем к ре­зульти­рующим усилиям, т.е. глав­ному вектору и главному мо­менту. Спроектировав глав­ный вектор на две взаимно перпендикулярные оси, одна из которых совпадает с осью балки, придем к знакомым из сопротивления материалов внутренним усилиям N и Q . Главный момент соответст­вует изгибающему моменту в рассматриваемом сечении Μ (рис. 2.7б).

Таким образом, основной нашей задачей является определение внутренних усилий Μ , Q и N исходя из уравнений равновесия, применяя их к той отсеченной части стержневой системы, к которой приложено меньшее число внешних усилий (включая опорные реакции) и проще геометрия.

Условно задачу определения внутренних усилий можно разбить на два этапа:

1. Определение реакций опор, при помощи которых сооружение связано с основанием и реакций связей отдельных жестких дисков друг с другом.

2. Определение внутренних усилий и построение их эпюр.

Определение реакций опор и связей.

Несмотря на то, что определение реакций опор и связей не является основной задачей расчета стержневой системы, тем не ме­нее, это чрезвычайно ответственный этап. Следует при этом отме­тить, что для определения внут­ренних усилий и построения их эпюр не во всех случаях обяза­тельно определение всех реакций опор и связей. Наиболее ярко это проявляется при расчете защем­ленной балки (ломаного стержня) (рис.2.8). Действи­тельно, при определении внут­ренних усилий в любом сечении всегда можно рассмотреть ту от­сеченную часть, которая не содержит реакций опор.

При нахождении реакций опор и связей необходимо стремиться к про­стоте выражений уравнений равнове­сия, избегая их вычисления из решения больших систем уравнений (при расчете вручную). Все сказанное спра­ведливо при разработке алгоритма рас­чета стержневых систем вручную.

Покажем на примере возможные приемы, упрощающие определение ре­акций опор и связей. Рассмотрим неко­торую раму с достаточно сложной гео­метрией (рис.2.9). В указанной раме возникают четыре реакции опор: V A , H A и V B , H B , да в каждом шарнире, при его расчленении - по две составляющие давления.

Таким образом, число искомых реакций опор и связей будет:

С 0 + 2Ш = 4 + 2  4 = 12

Если поступить формальным образом, то раму необходимо расчленить на отдельные жесткие диски и для каждого из них записать три уравнения равновесия. Рама состоит из 4-х дисков и

получим систему из 12 алгебраических уравнений, решив которую, найдем искомые реакции. Однако очевидна и сложность такого подхода – большая трудоемкость в решении системы уравнений.

Мы знаем, что внутренние усилия можно найти из равнове­сия любой из отсеченных частей, причем в отбрасываемой части могут быть и неизвестные опорные реакции или связи. Чтобы вос­пользоваться таким подходом, в нашем случае достаточно найти опорные ре­акции V A , H A и V B , H B , а также рас­крыть замкнутый контур. Для раскры­тия замкнутого контура надо провести сечение таким образом, чтобы рама распалась на две части. Причем сече­ние необходимо провести так, чтобы с одной стороны, было достаточно легко определить усилия в сечении (давления шарниров), а с другой – можно было определить внутренние усилия в лю­бом сечении рамы. Вполне очевидно, что таким условиям отвечает сечение проведенное через шарниры C и E (рис. 2.10). Не трудно заметить, что для определения внутренних усилий в лю­бом сечении достаточно знать восемь (а не 12 как в первом случае) реакций связей. Приведем алгоритм их опреде­ления. Рассматривая равновесие верх­ней части рамы, найдем:

Для проверки правильности вычисления реакций связей вос­пользуемся ранее не применявшимися уравнениями равновесия:

Следует отметить, что рациональное определение опорных реакций и связей требует определенных навыков, интуиции, что достигается в процессе решения достаточно большого числа задач.

3. Нахождение внутренних усилий и построение их эпюр.

Внутренние усилия M , Q и N в интересующем нас сечении стержня находятся из условия равновесия одной из отсеченных частей стержневой системы (левой или правой). Для наглядности изменения внутренних усилий в стержневой системе строят эпюры внутренних усилий, которые представляют собой графическое отображение характера распределения внутренних усилий. При их построении пользуются определенными правилами, встречавшимися нам сопротивлении материалов.

Дадим определения внутренних усилий, и порядок их вычислений.

Изгибающий момент - М в сечении равен алгебраической сумме моментов всех сил, действующих по одну сторону от сечения, относительно точки пересечения сечения с осью стержня.

Эпюра М . строится на растянутых волокнах стержня. Очер­тание эпюры М . имеет ряд особенностей, которые легко запомнить:

– на ненагруженном участке стержня эпюра М линейна;

– в точке приложения сосредоточенной силы эпюра Μ имеет излом в направлении силы;

– в точке приложения сосредоточенного момента в эпюре М будет скачок на величину момента;

– на участке с распределенной нагрузкой эпюра M . криво­линейна с выпуклостью в сторону действия нагрузки.

Поперечная сила Q в сечении равна алгебраической сумме проекций всех сил, действующих по одну сторону сечения, на нормаль к оси стержня.

Поперечная сила считается положительной, если вращает отсеченную часть по часовой стрелке.

Характер изменения эпюры Q связан с известной дифференциальной зависимостью с изгибающим моментом:

Следовательно:

– на ненагруженном участке эпюра Q постоянна;

– на участке, где действует равномерно распределенная нагрузка, эпюра Q линейна. Нулевому значению поперечной силы отвечает экстремальное значение изгибающего момента;

– в месте приложения сосредоточенной силы в эпюре Q будет скачок на величину этой силы.

Продольная (нормальная) сила N в сечении равна алгебраической сумме проекций всех сил, действующих по одну сторону сечения, на касательную к оси стержня в этом сечении.

В большинстве стержневых систем положительной считается растягивающая продольная сила. В арках положительной считается сжимающая сила.

В отношении очертания эпюры N можно сказать следующее:

На участке прямого стержня, свободном от внешней нагрузки, действующей вдоль оси стержня, эпюра N должна быть постоянна;

В месте приложения сосредоточенной силы вдоль оси стержня в эпюре N будет скачок на величину этой силы.

В рекомендованных учебниках , приведено достаточное число примеров задач подобных тем, которые включены в контрольную работу. Поэтому ниже даны лишь необходимые краткие методические указания к решению задач контрольной работы.

Первую задачу (задачи №№ 1-10) следует решить после изучения тем 1.1 и 1.2.

Во всех задачах рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В в каждой задаче приложены четыре силы, из которых две неизвестны. Можно избрать три способа решения: аналитический, графический и геометрический. Для данного типа задач целесообразно использовать аналитический способ решения.

Последовательность решения задачи :

1. Выбрать тело (точку), равновесие которого следует рассматривать.

2. Освободить тело (шарнир В ) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В , так как принято предполагать, что стержни растянуты.

3. Выбрать оси координат и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости ΣXi = 0; ΣУi ,=0. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно одной из неизвестных сил.

4. Определить реакции стержней из решения указанной системы уравнений.

5. Проверить правильность полученных результатов, решив уравнения равновесия относительно заново выбранных координат х и у .

Пример 1. Определить реакции стержней, удерживающих грузы F 1 = 70 кН и F 2 = 100 кН (рис. 1.1,а). Массой стержней пренебречь.

Решение .

1. Рассматриваем равновесие шарнира В (рис. 1.1,а).

Рисунок 1.1

2. Освобождаем шарнир В от связей и изображаем действующие из него активные силы и реакции связей (рис.1.1,б).

3. Выбираем систему координат, совместив ось у по направлению с реакцией R 2 (рис. 1,6) и составляем уравнения равновесия для системы сил, действующих на шарнир В :

4. Определяем реакции стержней R 1 и R 2 , решая уравнения (1), (2).

Из уравнения (1)

Подставляя найденное значение R 1 в уравнение (2), получаем

Знак минус перед значением R 2 указывает на то, что первоначально выбранное направление реакции неверное- следует направить реакцию R 2 в противоположную сторону, т.е. к шарниру В (на рис. 1,6 истинное направление реакции R 2 показано штриховым вектором).

5. Проверяем правильность полученных результатов, выбрав новое расположение осей координат х и у (рис. 1, в). Относительно этих осей составляем уравнения равновесия:

Из уравнения (3) находим R 2:

Подставляя найденное значение R 2 в уравнение (4), получаем:

Значения реакций R 1 и R 2 , полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.

Вторую задачу (задачи №№ 11–20) следует решать после изучения тем 1.3 и 1.4.

Во всех задачах требуется определить реакции опор балок. Студентам необходимо приобрести навыки определения реакций опор, так как с этого начинается решение многих задач по сопротив­лению материалов и деталям машин.

Последовательность решения задачи:

2. Выбрать расположение координатных осей, совместив ось х с балкой, а ось у направив перпендикулярно оси х .

3. Произвести необходимые преобразования заданных активных сил: силу, наклоненную к оси балки под углом α, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную нагрузку – ее равнодействующей, приложенной в середине участка распределения нагрузки.

4. Освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат.

5. Составить уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор.

6. Проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.

Пример 2. Определить реакции опор горизонтальной балки от заданной нагрузки.

Дано:

Схема балки (рис. 1.2). P = 20 кН, G = 10 кН, М = 4 кНм, q = 2 кН/м, a=2 м, b=3 м, .

Определить реакции опор в точках А и В .

Рисунок 1.2

Решение:

Рассмотрим равновесие балки АВ (рис. 1.3).

К балке приложена уравновешенная система сил, состоящая из активных сил и сил реакции.

Активные (заданные) силы:

Пара сил с моментом М ,