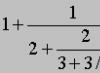Seringkali notasi yang lebih ringkas x 1 y 1 + x 2 y 2 + x 3 y 3 + … digunakan untuk pecahan lanjutan.

Bilangan x 1 y 1 = x 1 y 1 , x 1 y 1 + x 2 y 2 = x 1 y 1 + x 2 y 2 , x 1 y 1 + x 2 y 2 + x 3 y 3 = x 1 y 1 + x 2 y 2 + x 3 y 3 , ... disebut pecahan yang sesuai diberikan pecahan lanjutan. Jika suatu barisan pecahan yang sesuai mendekati suatu bilangan tertentu tanpa batas, maka dikatakan pecahan lanjutan tak terhingga menyatu ke nomor ini. Lebih tepatnya, pendekatan tak terbatas dari barisan bilangan a 1 a 2 ... ke bilangan a berarti, sekecil apa pun bilangan positif yang kita ambil, semua elemen barisan, mulai dari bilangan tertentu, akan berlokasi dari bilangan a pada jarak kurang dari ε. Konvergensi suatu barisan ke suatu bilangan biasanya dilambangkan sebagai berikut: lim s → ∞ a s = a.

Kami tidak akan mempelajari masalah yang paling menarik dalam mempelajari konvergensi pecahan lanjutan. Sebaliknya, kami menetapkan tugas untuk menghitung secara algoritmik urutan pecahan yang sesuai untuk pecahan lanjutan tertentu. Dengan melihat barisan ini, yang dihitung di komputer, Anda dapat membuat hipotesis tentang konvergensi pecahan lanjutan.

Anda dapat menganggap pecahan yang sesuai sebagai fungsi yang didefinisikan pada ruang barisan pasangan bilangan: f ⁡ x 1 y 1 x 2 y 2 … x n y n = x 1 y 1 + x 2 y 2 + x 3 y 3 + … + x n y n . Alangkah baiknya jika fungsi ini ternyata induktif atau ekstensi induktifnya dapat ditemukan.

Contoh lain: 1 1 + 1 1 + 1 1 + ... Dengan asumsi pecahan ini konvergen ke bilangan a, kita temukan bilangan ini. Untuk melakukan ini, perhatikan bahwa a = 1 1 + a (periksa!). Persamaan ini mempunyai dua solusi, yang mana solusi positifnya adalah a = 5 − 1 2 . Ngomong-ngomong, a = 1 φ = φ − 1 = 0,61803398874989…, dimana φ adalah bilangan Phidias dari bab 9. “ Angka Fibonacci". Pecahan lanjutan itu sendiri berhubungan langsung dengan bilangan Fibonacci: bilangan tersebut ditempatkan dengan tepat pada pembilang dan penyebut pecahan yang sesuai 1, 1 2, 2 3, 3 5, 5 8, 8 13, ....

Perlu dicatat bahwa metode penalaran yang digunakan untuk menemukan nilai pecahan lanjutan yang benar mengandung kelemahan yang signifikan. Dengan alasan yang persis sama, kita telah menemukan di bagian “Metode perhitungan perkiraan bilangan π” “nilai” dari jumlah tak terhingga 1 − 1 + 1 − 1 + 1 − … = 1 2. Sungguh aneh bahwa jumlah bilangan bulat ternyata merupakan pecahan. Rumus jumlah barisan geometri tak hingga dengan penyebut − 1 menghasilkan hasil yang sama: S = 1 1 − − 1 = 1 2 . Namun, jangan lupa bahwa rumus jumlah barisan geometri tak hingga hanya berlaku untuk penyebut yang nilai absolutnya kurang dari satu.

Mari kita tunjukkan hasil yang lebih aneh lagi, yang sekali lagi dikonfirmasi oleh rumus jumlah barisan geometri tak hingga: S = 1 + 2 + 4 + 8 + 16 + … = 1 + 2 ⁢ 1 + 2 + 4 + 8 + … = 1 + 2 ⁢ S, maka S = − 1, yaitu jumlah suku-suku positifnya ternyata negatif! Soalnya pencarian jumlah itu dilakukan dengan asumsi keberadaannya. Untuk melengkapi gambarannya, kita harus mempertimbangkan kasus lain ketika jumlahnya tidak ada, tetapi kita tidak akan mendapatkan hasil apa pun.

Bilangan yang sangat penting dalam matematika, e = 2.718281828459045..., mempunyai banyak nama: basis logaritma natural, nomor Makasar , bilangan Euler . Mustahil untuk membuat daftar situasi ketika angka ini muncul dalam matematika, yang, terlebih lagi, berfungsi sebagai pengingat abadi akan hari ulang tahun L. N. Tolstoy. Biasanya e ditentukan menggunakan batas indah kedua

Seperti bilangan π, bilangan Napier memiliki beberapa representasi indah dalam bentuk pecahan lanjutan: e − 2 = 1 1 + 1 2 1 + 1 3 1 + 1 4 1 + … = 2 2 + 3 3 + 4 4 + 5 5 + … = 1 1 + 1 2 + 1 1 + 1 1 + 1 4 + 1 1 + 1 1 + 1 6 + 1 1 + 1 1 + 1 8 + 1 1 + 1 1 + 1 10 + …

Bagi pembaca yang tertarik dengan pecahan lanjutan, kami merekomendasikan brosurnya.

Rencana:

Perkenalan

• 1 Ekspansi pecahan lanjutan
• 2 Pecahan yang Cocok
• 3 Perkiraan bilangan real dengan bilangan rasional
  • 3.1 Contoh
• 4 Properti dan contoh
• 5 Penerapan pecahan lanjutan
  • 5.1 Teori kalender
  • 5.2 Memecahkan perbandingan tingkat pertama
  • 5.3 Aplikasi lain
    • 5.3.1 Sifat-sifat rasio emas
• 6 Referensi sejarah
• 7 Motivasi
Catatan

Perkenalan

Pecahan lanjutan(atau pecahan lanjutan) adalah ekspresi matematika dari bentuk

Di mana A 0 adalah bilangan bulat dan yang lainnya A N bilangan asli (yaitu bilangan bulat non-negatif). Bilangan real apa pun dapat direpresentasikan sebagai pecahan lanjutan (berhingga atau tak terbatas). Suatu bilangan dapat direpresentasikan sebagai pecahan lanjutan berhingga jika dan hanya jika bilangan tersebut rasional. Suatu bilangan dinyatakan dengan pecahan lanjutan periodik jika dan hanya jika bilangan tersebut merupakan irasionalitas kuadrat.

1. Ekspansi pecahan lanjutan

Bilangan real apa pun X dapat diwakili oleh pecahan lanjutan (berhingga atau tak terhingga), di mana

di mana menunjukkan bagian bilangan bulat dari bilangan tersebut X .

Untuk bilangan rasional X perluasan ini akan berakhir ketika mencapai nol X N untuk beberapa n. Pada kasus ini X diwakili oleh pecahan lanjutan yang terbatas.

Untuk yang tidak rasional X semua kuantitas X N akan menjadi bukan nol dan proses perluasan dapat dilanjutkan tanpa batas waktu. Pada kasus ini X tampaknya merupakan pecahan lanjutan yang tak terhingga.

Untuk bilangan rasional, algoritma Euclidean dapat digunakan untuk memperoleh perluasan pecahan lanjutan dengan cepat.

2. Mencocokkan pecahan

N-Aduh pecahan yang sesuai untuk pecahan lanjutan disebut pecahan lanjutan berhingga yang nilainya sama dengan suatu bilangan rasional. Mencocokkan pecahan yang bilangan genapnya membentuk barisan menaik yang limitnya adalah X. Demikian pula, pencocokan pecahan berbilangan ganjil membentuk barisan menurun yang limitnya juga sama X .

Euler menurunkan rumus perulangan untuk menghitung pembilang dan penyebut pecahan yang sesuai:

Jadi, jumlahnya P N Dan Q N diwakili oleh nilai kontinu:

Urutannya semakin meningkat.

Pembilang dan penyebut pecahan yang berdekatan dihubungkan dengan hubungan:

yang dapat ditulis ulang dalam bentuk

Dari situlah berikut ini

3. Pendekatan bilangan real dengan bilangan rasional

Pecahan lanjutan memungkinkan Anda menemukan perkiraan rasional yang baik untuk bilangan real secara efisien. Yaitu jika bilangan real X diperluas menjadi pecahan lanjutan, maka pecahan yang sesuai akan memenuhi pertidaksamaan tersebut

Oleh karena itu, khususnya, berikut ini:

3.1. Contoh

• Mari kita uraikan bilangan π =3.14159265... menjadi pecahan lanjutan dan hitung pecahan yang sesuai: 3, 22/7, 333/106, 355/113, 103993/33102, ...

4. Sifat dan contohnya

• Bilangan rasional apa pun dapat direpresentasikan sebagai pecahan lanjutan berhingga dengan dua cara, misalnya:

• teorema Lagrange: Suatu bilangan direpresentasikan sebagai pecahan lanjutan periodik tak hingga jika dan hanya jika bilangan tersebut merupakan solusi irasional dari persamaan kuadrat dengan koefisien bilangan bulat.

untuk nomor

• Angka pi tidak memiliki pola yang sederhana:

• Teorema Gauss-Kuzmin: Untuk hampir semua (kecuali himpunan ukuran nol) bilangan real, terdapat rata-rata geometrik dari koefisien pecahan lanjutannya, dan sama dengan konstanta Khinchin.
• Teorema Marshall Hall. Jika dalam perluasan angka X pada pecahan lanjutan, mulai dari unsur kedua tidak ada bilangan yang lebih besar N, lalu mereka mengatakan nomor itu X milik kelas F(N). Bilangan real apa pun dapat direpresentasikan sebagai jumlah dari dua bilangan dari kelas tersebut F(4) dan berupa hasil kali dua bilangan dari kelasnya F(4). Kemudian ditunjukkan bahwa bilangan real apa pun dapat direpresentasikan sebagai penjumlahan dari 3 bilangan dari kelas tersebut F(3) dan sebagai penjumlahan 4 angka dari kelas F(2). Jumlah suku yang diperlukan dalam teorema ini tidak dapat dikurangi - untuk menyatakan beberapa bilangan dengan cara ini, jumlah suku yang lebih kecil saja tidak cukup.

5. Penerapan pecahan lanjutan

5.1. Teori kalender

Saat mengembangkan kalender matahari, perlu dicari perkiraan rasional jumlah hari dalam setahun, yaitu sebesar 365.2421988... Mari kita hitung pecahan yang cocok untuk bagian pecahan dari bilangan ini:

Pecahan pertama berarti setiap 4 tahun Anda perlu menambahkan satu hari ekstra; Prinsip ini menjadi dasar kalender Julian. Dalam hal ini, kesalahan 1 hari terakumulasi selama 128 tahun. Nilai kedua (29/7) tidak pernah digunakan. Pecahan ketiga (8/33), yaitu 8 tahun kabisat dalam jangka waktu 33 tahun, diusulkan oleh Omar Khayyam pada abad ke-11 dan menandai dimulainya kalender Persia, di mana kesalahan per hari terakumulasi selama 4500 tahun. (dalam Gregorian - lebih dari 3280 tahun). Versi yang sangat akurat dengan pecahan keempat (31/128, kesalahan per hari terakumulasi hanya selama 100.000 tahun) dipromosikan oleh astronom Jerman Johann von Medler (1864), tetapi tidak menarik banyak minat.

5.2. Memecahkan perbandingan tingkat pertama

Mari kita pertimbangkan perbandingannya: , dimana diketahui, dan kita dapat berasumsi demikian A timbal balik hanya dengan M. Perlu menemukan X .

Mari kita kembangkan menjadi pecahan lanjutan. Ini akan menjadi pecahan terakhir, dan pecahan terakhir yang cocok adalah . Mari kita substitusikan ke dalam rumus (1):

Ini mengikuti dari ini:

Kesimpulan: kelas residu adalah solusi dari perbandingan awal.

5.3. Aplikasi lain

5.3.1. Sifat-sifat rasio emas

Hasil menarik yang dihasilkan dari fakta bahwa ekspresi pecahan lanjutan untuk φ tidak menggunakan bilangan bulat lebih besar dari 1 adalah bahwa φ adalah salah satu bilangan real yang "paling sulit" untuk didekati menggunakan bilangan rasional. Salah satu teorema (Teorema Hurwitz) menyatakan bahwa bilangan real apa pun k dapat didekati dengan pecahan M/N dengan bantuan

Lalu ketika hampir semua bilangan real k pada akhirnya memiliki banyak perkiraan yang tak terhingga banyaknya M/N, yang terletak pada jarak yang jauh lebih kecil dari k dari batas ini, perkiraan untuk φ (yaitu angka 5/3, 8/5, 13/8, 21/13, dll.) berturut-turut "menyentuh batas", menjaga jarak hampir persis pada jarak dari φ , sehingga tidak pernah menghasilkan perkiraan yang mengesankan seperti, misalnya, 355/113 untuk π. Dapat ditunjukkan bahwa sembarang bilangan real yang berbentuk ( A + Bφ)/( C + Dφ) – dimana A, B, C Dan D adalah bilangan bulat seperti iklan − SM= ±1 – memiliki sifat yang sama dengan rasio emas φ; dan juga bahwa semua bilangan real lainnya dapat diperkirakan dengan lebih baik.

6. Latar belakang sejarah

Matematikawan kuno mampu merepresentasikan hubungan besaran yang tidak dapat dibandingkan dalam bentuk rantai hubungan yang berurutan, memperoleh rantai ini menggunakan algoritma Euclid. Rupanya, dengan cara inilah Archimedes memperoleh perkiraannya - ini adalah pecahan ke-12 yang sesuai untuk atau dari pecahan ke-4 yang sesuai untuk .

Pada abad ke-5, matematikawan India Aryabhata menggunakan "metode penggilingan" serupa untuk menyelesaikan persamaan tak tentu derajat pertama dan kedua. Dengan menggunakan teknik yang sama, perkiraan yang terkenal untuk bilangan π (355/113) mungkin diperoleh. Pada abad ke-16, Raphael Bombelli mengekstraksi akar kuadrat menggunakan pecahan lanjutan (lihat algoritmanya).

Teori modern tentang pecahan lanjutan didirikan pada tahun 1613 oleh Pietro Antonio Cataldi. Dia mencatat sifat utamanya (posisi antara pecahan yang sesuai) dan memperkenalkan notasi yang mengingatkan pada notasi modern. Teorinya kemudian diperluas oleh John Wallis, yang menciptakan istilah tersebut "pecahan lanjutan". Istilah yang setara adalah " pecahan lanjutan"muncul pada akhir abad ke-18.

Pecahan ini digunakan terutama untuk perkiraan rasional bilangan real; misalnya, Christiaan Huygens menggunakannya untuk merancang roda gigi planetariumnya. Huygens telah mengetahui bahwa pecahan yang sesuai selalu tidak dapat direduksi dan mewakili perkiraan rasional terbaik.

Pada abad ke-18, teori pecahan lanjutan diselesaikan secara umum oleh Leonhard Euler dan Joseph Louis Lagrange.

7. Motivasi

Pecahan lanjutan adalah representasi bilangan real yang paling "alami secara matematis".

Kebanyakan orang akrab dengan representasi desimal dari bilangan real, yang dapat didefinisikan sebagai

dimana a 0 dapat berupa bilangan bulat apa saja, dan selanjutnya a i adalah salah satu elemen (0,1,2,…,9). Dalam representasi ini, bilangan π, misalnya, dapat direpresentasikan sebagai barisan bilangan bulat.

Representasi desimal ini memiliki beberapa masalah. Salah satunya adalah banyak bilangan rasional yang tidak mempunyai representasi berhingga dalam sistem ini. Misalnya, bilangan 1/3 dapat diwakili oleh barisan tak terhingga (0,3,3,3,3,...). Masalah lainnya adalah bahwa konstanta 10 pada dasarnya adalah pilihan arbitrer yang mengutamakan bilangan yang terkait dengan bilangan bulat 10. Misalnya, 137/1600 mempunyai representasi desimal berhingga, sedangkan 1/3 tidak, karena 137/1600 adalah lebih sederhana dari 1/3, tetapi hanya karena 1600 membagi pangkat 10 (10 6 = 1600 × 625). Notasi sebagai pecahan lanjutan merupakan representasi bilangan real yang tidak mempunyai permasalahan tersebut.

Mari kita lihat bagaimana kita mendeskripsikan bilangan seperti 415/93, yang kira-kira sama dengan 4,4624. Sekitar 4. Sebenarnya lebih dari 4, sekitar 4 + 1/2. Namun angka 2 pada penyebutnya tidak sepenuhnya akurat; harus ada angka yang sedikit lebih besar dari 2, kira-kira 2 + 1/6. Jadi 415/93 kira-kira sama dengan 4 + 1/(2 + 1/6). Namun angka 6 pada penyebutnya salah; nilai sebenarnya sedikit lebih dari 6,6+1/7. Jadi 415/93 adalah 4+1/(2+1/(6+1/7). Ini adalah nilai pastinya.

Dengan menghilangkan beberapa bagian yang diperlukan dalam ekspresi 4 + 1 / (2 + 1 / (6 + 1 / 7)) kita mendapatkan notasi singkat. (Perhatikan bahwa merupakan praktik umum untuk mengganti hanya koma pertama dengan titik koma.)

Representasi sebagai pecahan lanjutan dari bilangan real dapat didefinisikan dengan cara ini. Ia memiliki beberapa sifat yang diinginkan:

• Representasi sebagai pecahan lanjutan berhingga jika dan hanya jika bilangan tersebut rasional.

• Setiap bilangan rasional pada dasarnya memiliki representasi unik sebagai pecahan lanjutan. Setiap bilangan rasional dapat direpresentasikan dengan dua cara, karena [ A 0 ; A 1 , … A N − 1 , A N ] = [A 0 ; A 1 , … A N − 1 , A N− 1, 1]. Matematikawan lebih memilih korespondensi satu-satu antara bilangan rasional dan pecahan lanjutan; notasi pertama yang lebih pendek dipilih sebagai representasi kanonik.

• Representasi sebagai pecahan lanjutan dari bilangan irasional adalah unik.

• Pecahan lanjutan bersifat periodik jika dan hanya jika bilangan tersebut merupakan irasionalitas kuadrat, yaitu. memiliki bentuk

untuk bilangan bulat A, B, C, D; Di mana B Dan D bukan nol dan C>1 dan C bukan persegi eksak.

Misalnya, pecahan lanjutan periodik adalah rasio emas, dan pecahan lanjutan periodik adalah akar kuadrat dari 2.

• Pemotongan awal representasi pecahan lanjutan dari x menghasilkan perkiraan rasional terhadap x, yang dalam arti tertentu merupakan perkiraan rasional "terbaik".

Properti terakhir ini sangat penting. Representasi desimal suatu angka tidak memilikinya. Memotong representasi desimal suatu bilangan akan menghasilkan perkiraan bilangan yang masuk akal, namun biasanya bukan perkiraan yang sangat baik. Misalnya, pemotongan 1/7 = 0,142857... di tempat berbeda menghasilkan perkiraan seperti 142/1000, 14/100, dan 1/10. Namun yang jelas perkiraan rasional terbaik adalah angka “1/7” itu sendiri. Dengan memotong representasi desimal π kita mendapatkan perkiraan seperti 31415/10000 dan 314/100. Pecahan lanjutan π dimulai dengan . Dengan memotong representasi ini kita mendapatkan perkiraan rasional yang sangat baik 3, 22/7, 333/106, 355/113, 103993/33102,…. Penyebut 314/100 dan 333/106 hampir sama, namun kesalahan pada perkiraan 314/100 sembilan belas kali lebih besar daripada kesalahan pada perkiraan 333/106. Sebagai perkiraan π, perkiraan 3,1416 lebih dari seratus kali lebih akurat.

BADAN KEHUTANAN FEDERAL RF

FBOU SPO "DIVNOGORSKY KEHUTANAN - TEKNIK"

KANTOR MATEMATIKA

LAPORAN

TENTANG PEKERJAAN PENELITIAN NO.

PADA TOPIK "FRAKSI LANJUTAN"

Lengkap:

mahasiswa tahun pertama gr. 11B-L Kardapoltsev A.O.

Diperiksa:

Guru: Konovalova E.G.

Nilai:

Pendahuluan - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 3

Pecahan lanjutan - - - - - - - - - - - - - - - - - - - - - - - - - - - - 4

Pemuaian pecahan lanjutan - - - - - - - - - - - - - - - - - - - - - 5

Perkiraan bilangan real dengan bilangan rasional - - 6

Latar Belakang Sejarah - - - - - - - - - - - - - - - - - - - - - - - - - - 7

Kesimpulan - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 8

Daftar Pustaka - - - - - - - - - - - - - - - - - - - - - - - 9

Perkenalan

Tujuan dari penelitian saya adalah untuk mempelajari teori pecahan lanjutan. Di dalamnya saya akan mencoba mengungkap sifat-sifat pecahan yang sesuai, ciri-ciri pemuaian bilangan real menjadi pecahan biasa, kesalahan-kesalahan yang timbul akibat pemuaian tersebut, dan penerapan teori pecahan lanjutan untuk menyelesaikan suatu bilangan. masalah aljabar.

Pecahan lanjutan diperkenalkan pada tahun 1572 oleh matematikawan Italia, Bombelli. Notasi modern untuk pecahan lanjutan ditemukan oleh matematikawan Italia Cataldi pada tahun 1613. Matematikawan terhebat abad ke-18, Leonardo Euler, adalah orang pertama yang menguraikan teori pecahan lanjutan, mengajukan pertanyaan tentang penggunaannya untuk menyelesaikan persamaan diferensial, menerapkannya pada perluasan fungsi, merepresentasikan hasil kali tak hingga, dan memberikan generalisasi penting. dari mereka.

Karya Euler tentang teori pecahan lanjutan dilanjutkan oleh M. Sofronov (1729-1760), akademisi V.M. Viskovaty (1779-1819), D. Bernoulli (1700-1782), dll. Banyak hasil penting dari teori ini dimiliki oleh ahli matematika Prancis Lagrange, yang menemukan metode untuk penyelesaian perkiraan persamaan diferensial menggunakan pecahan lanjutan.

Pecahan lanjutan

Pecahan lanjutan(atau pecahan lanjutan) adalah ekspresi matematika dari bentuk

Di mana A 0 ada bilangan bulat dan yang lainnya A N bilangan asli (yaitu bilangan bulat non-negatif). Bilangan real apa pun dapat direpresentasikan sebagai pecahan lanjutan (berhingga atau tak terbatas). Suatu bilangan dapat direpresentasikan sebagai pecahan lanjutan berhingga jika dan hanya jika bilangan tersebut rasional. Suatu bilangan dinyatakan dengan pecahan lanjutan periodik jika dan hanya jika bilangan tersebut merupakan irasionalitas kuadrat.

Ekspansi pecahan lanjutan

Bilangan real apa punX dapat diwakili oleh pecahan lanjutan (berhingga atau tak terhingga) di mana

di mana menunjukkan bagian bilangan bulat dari bilangan tersebutX .

Untuk bilangan rasionalX perluasan ini akan berakhir ketika mencapai nolX N untuk beberapa N. Pada kasus ini X diwakili oleh pecahan lanjutan yang terbatas

Untuk yang tidak rasionalX semua kuantitas X N akan menjadi bukan nol dan proses perluasan dapat dilanjutkan tanpa batas waktu. Pada kasus iniX tampaknya merupakan pecahan lanjutan yang tak terhingga

Perkiraan bilangan real dengan bilangan rasional

Pecahan lanjutan memungkinkan Anda menemukan perkiraan rasional yang baik untuk bilangan real secara efisien. Yaitu jika bilangan realX diperluas menjadi pecahan lanjutan, maka pecahan yang sesuai akan memenuhi pertidaksamaan:

Oleh karena itu, khususnya, berikut ini:

1) pecahan yang sesuaiadalah perkiraan terbaik

Untuk X di antara semua pecahan yang penyebutnya tidak melebihiQ N ;

2) ukuran irasionalitas suatu bilangan irasional tidak kurang dari 2.

Contoh

1) Mari kita perbanyak jumlahnyaπ =3.14159265... menjadi pecahan lanjutan dan hitung pecahan yang bersesuaian: 3, 22/7, 333/106, 355/113, 103993/33102, ...

Pecahan kedua (22/7) adalah pendekatan Archimedean yang terkenal. Yang keempat (355/113) pertama kali diperoleh di Tiongkok Kuno.

2) Dalam teori musik perlu dicari pendekatan yang rasional

Pecahan ketiga yang sesuai: 7/12 memungkinkan kita membenarkan pembagian klasik oktaf menjadi 12 seminada.

Referensi sejarah

Matematikawan kuno mampu merepresentasikan hubungan besaran yang tidak dapat dibandingkan dalam bentuk rantai hubungan yang berurutan, memperoleh rantai ini menggunakan algoritma Euclid. Rupanya, beginilah cara Archimedes mendapatkan perkiraannya:

Ini adalah pecahan ke-12 yang cocok untuk

Atau dari pecahan ke-4 yang cocok untuk.

Pada abad ke-5, matematikawan India Aryabhata menggunakan "metode penggilingan" serupa untuk menyelesaikan persamaan tak tentu derajat pertama dan kedua. Dengan menggunakan teknik yang sama, perkiraan umum untuk bilangan tersebut mungkin diperolehπ (355/113). Pada abad ke-16, Raphael Bombelli mengekstraksi akar kuadrat menggunakan pecahan lanjutan (lihat algoritmanya).

Teori modern tentang pecahan lanjutan didirikan pada tahun 1613 oleh Pietro Antonio Cataldi. Dia mencatat sifat utamanya (posisi antara pecahan yang sesuai) dan memperkenalkan notasi yang mengingatkan pada notasi modern. Teorinya kemudian diperluas oleh John Wallis, yang menciptakan istilah tersebut "pecahan lanjutan". Istilah yang setara adalah " pecahan lanjutan"muncul pada akhir abad ke-18.

Pecahan ini digunakan terutama untuk perkiraan rasional bilangan real; misalnya, Christiaan Huygens menggunakannya untuk merancang roda gigi planetariumnya. Huygens telah mengetahui bahwa pecahan yang sesuai selalu tidak dapat direduksi dan mewakili perkiraan rasional terbaik.

Pada abad ke-18, teori pecahan lanjutan diselesaikan secara umum oleh Leonhard Euler dan Joseph Louis Lagrange.

Kesimpulan

Makalah penelitian ini menunjukkan pentingnya pecahan lanjutan dalam matematika.

Mereka dapat berhasil diterapkan untuk menyelesaikan persamaan bentuk tak tentu

kapak+oleh=c.

Kesulitan utama dalam menyelesaikan persamaan tersebut adalah menemukan solusi tertentu. Jadi, dengan menggunakan pecahan lanjutan, Anda dapat menentukan algoritma untuk menemukan solusi tertentu.

Pecahan lanjutan juga dapat diterapkan untuk menyelesaikan persamaan tak tentu yang lebih kompleks, misalnya persamaan Pell:

().

Pecahan lanjutan tak hingga dapat digunakan untuk menyelesaikan persamaan aljabar dan transendental serta menghitung nilai fungsi individual dengan cepat.

Saat ini pecahan lanjutan semakin banyak digunakan dalam teknologi komputer, karena memungkinkan dibangunnya algoritma yang efektif untuk menyelesaikan sejumlah masalah di komputer.

Bibliografi:

http://ru.wikipedia.org

1. Aljabar dan teori bilangan. Diedit oleh N.Ya. Vilenkina, M, “Pencerahan”, 84.
2. MEREKA. Vinogradov. Dasar-dasar teori bilangan. M, “Ilmu Pengetahuan”, 72.
3. A A. Kocheva. Buku kerja praktis tentang aljabar dan teori bilangan. M, “Pencerahan”, 84.
4. L.Ya. Kulikov, A.I. Moskalenko, A.A. Fomin. Kumpulan soal aljabar dan teori bilangan. M, “Pencerahan”, 93.

E.S. Lyapin, A.E. Evseev. Aljabar dan teori bilangan. M, “Pencerahan”,

Uraian pekerjaan

Tujuan dari penelitian saya adalah untuk mempelajari teori pecahan lanjutan. Di dalamnya saya akan mencoba mengungkap sifat-sifat pecahan yang sesuai, ciri-ciri pemuaian bilangan real menjadi pecahan biasa, kesalahan-kesalahan yang timbul akibat pemuaian tersebut, dan penerapan teori pecahan lanjutan untuk menyelesaikan suatu bilangan. masalah aljabar.

Pecahan lanjutan - - - - - - - - - - - - - - - - - - - - - - - - - - - - 4

Pemuaian pecahan lanjutan - - - - - - - - - - - - - - - - - - - - - 5

Perkiraan bilangan real dengan bilangan rasional - - 6

Latar Belakang Sejarah - - - - - - - - - - - - - - - - - - - - - - - - - - 7

Kesimpulan - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 8

Daftar Pustaka - - - - - - - - - - - - - - - -

Suatu barisan yang setiap sukunya merupakan pecahan biasa akan menghasilkan pecahan lanjutan (atau lanjutan) jika suku keduanya dijumlahkan dengan suku pertama, dan setiap pecahan yang dimulai dari suku ketiga ditambahkan ke penyebut pecahan sebelumnya. Misalnya, barisan 1, 1/2, 2/3, 3/4, ..., n/(n + 1), ... menghasilkan pecahan lanjutan

Dimana elipsis di bagian akhir menunjukkan bahwa proses tersebut berlanjut tanpa batas waktu. Pada gilirannya, pecahan lanjutan memunculkan barisan pecahan lain yang disebut pecahan sesuai. Dalam contoh kita, pecahan pertama, kedua, ketiga, dan keempat adalah sama

Mereka dapat dibangun menggunakan aturan sederhana dari barisan hasil bagi tidak lengkap 1, 1/2, 2/3, 3/4, .... Pertama-tama, mari kita tuliskan pecahan pertama dan kedua yang sesuai 1/1 dan 3/2. Pecahan ketiga yang sesuai sama dengan (2*1 + 3*3)/(2*1 + 3*2) atau 11/8, pembilangnya sama dengan jumlah hasil kali pembilang cocok pertama dan kedua pecahan, masing-masing dikalikan dengan pembilang dan penyebut hasil bagi tidak lengkap ketiga, dan penyebutnya sama dengan jumlah hasil kali penyebut hasil bagi tidak lengkap pertama dan kedua, masing-masing dikalikan dengan pembilang dan penyebut hasil bagi tidak lengkap ketiga. Pecahan keempat yang sesuai diperoleh dengan cara yang sama dari hasil bagi tidak lengkap keempat 3/4 dan pecahan cocok kedua dan ketiga: (3*3 + 4*11)/(3*2 + 4*8) atau 53/38. Mengikuti aturan ini, kita menemukan tujuh pecahan pertama yang sesuai: 1/1, 3/2, 11/8, 53/38, 309/222, 2119/1522, dan 16687/11986. Mari kita tuliskan dalam bentuk pecahan desimal (dengan enam tempat desimal): 1.000000; 1.500.000; 1.375.000; 1.397368; 1.391892; 1.392247 dan 1.392208. Nilai pecahan lanjutan kita adalah bilangan x yang digit pertamanya adalah 1,3922. Pecahan yang pas adalah perkiraan terbaik dari x. Selain itu, angka-angka tersebut bergantian lebih kecil atau lebih besar dari bilangan x (ganjil lebih besar dari x, dan bilangan genap lebih kecil). Untuk menyatakan perbandingan dua bilangan bulat positif sebagai pecahan lanjutan berhingga, Anda perlu menggunakan metode pembagi persekutuan terbesar. Misalnya, ambil rasio 50/11. Karena 50 = 4Х11 + 6 atau 11/50 = 1/(4 + 6/11), dan demikian pula, 6/11 = 1/(1 + 5/6) atau 5/6 = 1/(1 + 1 / 5), kita mendapatkan:

Pecahan lanjutan digunakan untuk memperkirakan bilangan irasional ke bilangan rasional. Mari kita asumsikan bahwa x adalah bilangan irasional (artinya, x tidak dapat direpresentasikan sebagai perbandingan dua bilangan bulat). Maka jika n0 adalah bilangan bulat terbesar yang lebih kecil dari x, maka x = n0 + (x - n0), dimana x - n0 adalah bilangan positif kurang dari 1, maka inversnya x1 lebih besar dari 1 dan x = n0 + 1/x1. Jika n1 adalah bilangan bulat terbesar yang lebih kecil dari x1, maka x1 = n1 + (x1 - n1), dimana x1 - n1 adalah bilangan positif yang lebih kecil dari 1, sehingga inversnya x2 lebih besar dari 1, dan x1 = n1 + 1/x2 . Jika n2 adalah bilangan bulat terbesar yang lebih kecil dari x2, maka x2 = n2 + 1/x3, dimana x3 lebih besar dari 1, dst. Hasilnya, kita menemukan langkah demi langkah barisan hasil bagi tidak lengkap n0, 1/n1, 1/n2, ... dari pecahan lanjutan, yang merupakan perkiraan x. Mari kita jelaskan ini dengan sebuah contoh. Mari kita berpura-pura seperti itu

Https:="">
">

• - perbandingan dua bilangan dibagi satu sama lain, berbentuk a/b; misalnya 3/4. Dalam persamaan ini, a adalah pembilangnya dan b adalah penyebutnya. Jika a dan b bilangan bulat, maka hasil bagi adalah pecahan sederhana. Jika a lebih kecil dari b, maka pecahan tersebut adalah...

  Kamus ensiklopedis ilmiah dan teknis

• - praktik pembayaran komisi kepada perwakilan terdaftar setelah mereka berhenti beroperasi sebagai perantara/dealer atau kepada ahli waris setelah kematian perwakilan terdaftar...

  Kamus ekonomi besar

• - Perhitungan bunga, atau diskonto, pendapatan masa depan secara konstan. Pada tingkat tahunan 100 r, setelah N tahun jumlah pinjaman akan meningkat N kali lipat dibandingkan jumlah aslinya...

  Kamus ekonomi

• - Rukhin, 1961, - ritme yang tidak dipisahkan oleh jeda sedimentasi yang berkelanjutan dan tentu memiliki bagian regresif...

  Ensiklopedia Geologi

• - lingkungan di mana kecepatan rambat gelombang elastis terus meningkat seiring dengan kedalaman. Mempelajarinya dalam eksplorasi seismik memainkan peran besar...

  Ensiklopedia Geologi

• - lihat Hari dihitung secara berurutan...

  kamus kelautan

• - dalam perhitungan keuangan teoretis - bunga yang diperoleh dalam periode waktu yang sangat kecil Sinonim: Akrual berkelanjutan Lihat. Lihat juga: Biaya pinjaman  ...

  Kamus Keuangan

• - lihat Pecahan...
• - lihat Pecahan...

  Kamus Ensiklopedis Brockhaus dan Euphron

• - angka atau fungsi yang muncul ketika pecahan lanjutan dipecah...

  Ensiklopedia Besar Soviet

• - 1. Arch., Orel., Saudara. Menarilah sambil sesekali mengetukkan kaki Anda ke tanah. SRNG 8, 189; SOG 1989, 75; FSS, 12. 2.Volg. Mengetuk-ngetukkan kakimu karena kedinginan. Glukhov 1988, 3...
• - Saudara. Sama seperti mengalahkan pecahan 1. FSS, 53...

  Kamus besar ucapan Rusia

• - Gagal/gagalkan seseorang pada pecahan. Jarg. pejantan. Tolak, tolak seseorang. untuk alasan yang tidak penting. NRL-82; Mokienko 2003, 26...

  Kamus besar ucapan Rusia

• - adj., jumlah sinonim: 1 utuh...

  Kamus sinonim

"FRAKSI LANJUTAN" dalam buku

Pemilihan umum Putin yang berkelanjutan

Pemilihan umum Putin yang berkelanjutan Untuk mempertahankan popularitas pribadi Putin di kalangan masyarakat, timnya segera bereaksi terhadap perubahan sekecil apa pun dalam situasi tersebut. “Pemilu permanen” menjadi semakin penting pada awal tahun 2000an, ketika serangkaian “revolusi warna” menyapu bersih negara-negara di dunia.

Inovasi yang berkelanjutan dan radikal

Inovasi yang berkelanjutan dan radikal Saat ini, semua orang sudah familiar dengan teori kurva pertumbuhan. Selama bertahun-tahun, ini telah (dan terus menjadi) salah satu alat yang memungkinkan kita menentukan posisi suatu perusahaan pada setiap tahap perkembangannya. Setiap produk dan layanan memiliki siklusnya sendiri

4. 5. Aliran terus menerus

4. 5. Aliran kontinu Saat membangun model sistem distribusi industri, kita berasumsi bahwa dasarnya - setidaknya pada awalnya - adalah aliran kontinu dan interaksi variabel. Kebijaksanaan peristiwa dapat diperhitungkan ketika menganalisis sistem informasi dengan

Inovasi berkelanjutan dan kesuksesan berkelanjutan adalah hadiah bagi pemenangnya

Inovasi Berkelanjutan dan Kesuksesan Berkelanjutan adalah Hadiah bagi Pemenangnya Sekarang setelah Anda memahami masing-masing dari tiga sisi segitiga kesuksesan, saya akan menggabungkannya. Jika tujuan Anda adalah menciptakan perusahaan yang dapat terus berinovasi dan menerapkan

Ancaman terus menerus

Ancaman terus menerus Sepanjang malam itu kami berada di bawah todongan senjata dengan pihak Rusia. Mereka mengunci kami, dan kemudian yang lain datang dan mengutuk bahwa pintunya ditutup. Semacam gerakan tidak berhenti, segala sesuatu terguncang dan diperiksa: peti, kotak, kotak. Isinya dibuang

Bab I. KONFLIK TERUS-MENERUS DAN gencatan senjata yang TIDAK DAPAT DIANDALKAN

BAB I. KONFLIK TERUS-MENERUS DAN gencatan senjata yang TIDAK DAPAT DIANDALKAN Pada tahun 1559, pukulan tombak Montgomery, yang membunuh Raja Henry II, “mengubah wajah Prancis”. Akankah pewaris takhta, Francis II, mampu mengekang kekuatan yang siap mengamuk jika kekuasaan kerajaan melemah sedikit pun? Di satu sisi,

Pecahan yang Cocok

3.2.1. Pecahan biner

3.2.1. Pecahan Biner Pertama, sedikit matematika. Di sekolah kita mempelajari dua jenis pecahan: sederhana dan desimal. Desimal pada dasarnya adalah perluasan suatu bilangan menjadi pangkat sepuluh. Jadi, penulisan 13.6704 berarti bilangan yang sama dengan 1?101 + 3?100 + 6?10-1 + 7?10-2 + ​​​​0?10-3 + 4?10-4. Tetapi

3.2.5. Pecahan tak terbatas

3.2.5. Pecahan tak hingga Dari sekolah kita semua ingat bahwa tidak semua bilangan dapat ditulis sebagai pecahan desimal hingga. Ada dua jenis pecahan tak hingga: periodik dan non-periodik. Contoh pecahan tak periodik adalah bilangan?, pecahan periodik adalah bilangan? atau lainnya

Upaya Panjang dan Berkelanjutan yang Dapat Dilakukan

Apa yang bisa dicapai oleh upaya jangka panjang dan berkelanjutan? Apakah permainan ini sepadan dengan usahanya? Oh ya! Buku tersebut akhirnya terjual 8 juta eksemplar dalam 39 bahasa. Apakah itu terjadi dalam semalam? Oh tidak! Kami berhasil masuk dalam daftar buku terlaris setahun setelah buku tersebut diterbitkan—selesai

Pecahan

Pecahan Pecahan adalah lembaga baru yang menawarkan pelajaran matematika. Desainer Freddie Matisse menyajikan pilihan logo agensi sebagai sebuah teka-teki: A menjadi B melalui transformasi sederhana; jika Anda melakukan transformasi yang sama untuk segi lima

Ciri keenam: gerakannya terhubung dan berkesinambungan dengan pembentukan satu qi

Ciri keenam: gerakan-gerakan yang sambung-menyambung dan berkesinambungan dengan terbentuknya qi tunggal Risalah tentang senam memberikan syarat-syarat sebagai berikut: 1) Gerakan maju mundur harus ada jeda dan perubahan. Maju dan mundur pasti ada revolusi.2) Setelah dipungut, mereka segera melepaskannya,

Inovasi Berkelanjutan

Inovasi Berkelanjutan Pasar dan teknologi terus berubah dan ketika produk-produk sukses tidak digunakan lagi. Bahkan perusahaan terkuat pun sangat rentan terhadap perubahan teknologi dan pasar. Oleh karena itu, untuk mempertahankan kepemimpinan pasar, perusahaan

Inovasi Berkelanjutan: Umpan Balik

Inovasi Berkelanjutan: Umpan Balik Pengalaman Intel menunjukkan bahwa inovasi berkelanjutan tidak hanya menghalangi pesaing, namun juga menghasilkan keuntungan bagi inovasi baru. Pasar mikroprosesor jauh lebih dinamis dibandingkan pasar sistem pencukur. Gambar 7-3 mengilustrasikan trennya

1.4. Sistem diskrit dan kontinu